2차원으로 바라본 3차원

우리는 3차원 공간에 살고 있다. 덕분에 애석하게도 3차원 공간(엄밀하게는, 3-manifold)의 전체적인 모습을 바라볼 수는 없다. 물론 Thurston 선생님은 가능했을 것 같지만... 반면 2차원 공간, 즉 곡면의 전체적인 형태를 바라보는 것은 가능하고, closed orientable surfaces의 위상 구조에 대해서는 이미 이해하고 있다.

이러한 맥락에서, 자연스레 우리는 곡면을 통해 특정 3차원 공간을 이해보려고 시도할 수 있다. 예를 들어, 원 $S^1$을 살짝 부풀려서 원기둥 $S^1 \times [0, 1]$을 만들고, 원 사이의 homeomorphism $f : S^1 \to S^1$을 이용하여 원기둥의 양 끝을 비틀어 붙일 수 있다. 즉, $S^1 \times [0, 1] / (x, 0) \sim (f(x), 1)$을 생각하여 아래와 같이 topological torus를 얻을 수 있다.

Gluing $S^1 \times [0, 1]$

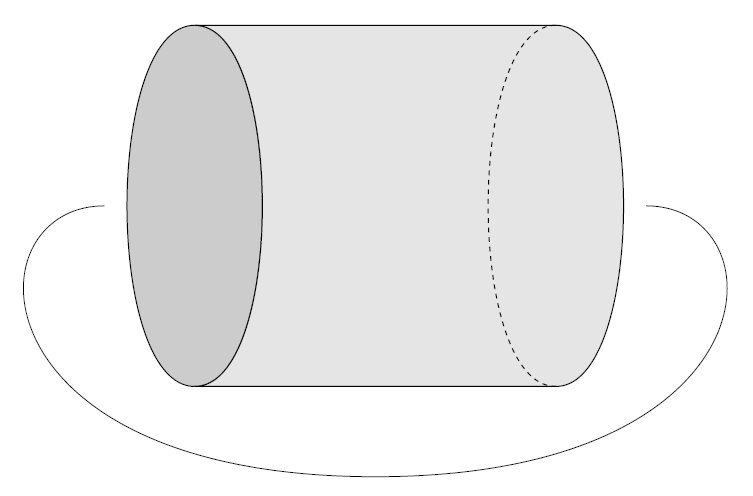
비슷한 일을 곡면에 대해서도 할 수 있다. 즉, 곡면 $S$와 homeomorphism $f: S \to S$에 대해서 $$M_f = S \times [0, 1] / (x, 0) \sim (f(x), 1)$$을 생각할 수 있는데, 결과적으로 $M_f$는 closed 3-manifold가 되고 이를 mapping torus with monodromy $f$라고 한다.

요즘의 나는 이런 mapping torus를 이해하려고 한다. 특히, Thurston의 hyperbolization theorem에 따르면 generic 한 monodromy (pseudo-Anosov)에 대해서 mapping torus가 쌍곡 기하구조를 가질 수 있다. 더불어 Mostow rigidity theorem에 의해 이러한 쌍곡 기하구조는 유일하다. 이렇듯 mapping torus가 가지고 있는 구조가 풍부하기 때문에, 흥미로운 관찰을 많이 할 수 있을 것이라 기대하고 있다.

하지만 역으로, 3차원에서 시작해서 이러한 구조를 찾을 수 있을까? 즉, 어떤 hyperbolic 3-manifold가 주어졌을 때 이것이과연 mapping torus로서 얻어질 수 있는 것인지, 그렇다면 그 monodromy는 어떻게 찾을 수 있을지 알 수 있을까? Thurston은 1st cohomology에 어떤 norm을 정의하여 이 문제에 답을 하였다.

$M$이 hyperbolic 3-manifold라고 하자. 그럼 integral cohomology class $\alpha \in H^1(M;\mathbb{Z})$에 대해서, 이것의 Poincare dual surface의 오일러 지표를 이용하여 값을 대응시킬 수 있다. 이러한 대응은 결국 $H^1(M;\mathbb{R})$에 norm을 정의하는데, 자세한 것은 https://en.wikipedia.org/wiki/Thurston_norm를 참고하길 바란다.

이 norm을 Thurston norm이라고 하는데, 흥미로운 것은 이 norm의 값이 1인 일종의 구면을 생각하면 이는 유한다면체가 된다는 것이다. 그리고 Thurston은 이 유한 다면체의 각 면이 정의하는 cohomology space의 각 원뿔에 대해서 원뿔의 모든 primitive integral element가 mapping torus 구조를 정의하는 monodromy이거나 혹은 모두 그렇지 않음을 증명하였다. cohomology class가 어떻게 monodromy에 대응되는지는 mapping torus가 surface bundle over the circle이라는 것에 착안하는데, 자세한 것은 생략한다.

한 hyperbolic 3-manifold가 가질 수 있는 monodromy defining mapping torus의 성질 역시 요즘 관심있게 들여다보고 있는 방향이기도 하다.

3차원을 이와같이 2차원으로 이해하려는 시도에 대해 또 하나 던질 수 있는 질문은, 과연 mapping torus로 얻어지는 3-manifold가 진짜로 많냐는 것이다. 즉, Thurston norm의 unit ball을 생각해서 얻는 원뿔들 중 적어도 하나가 mapping torus structure를 주는 경우가 얼마나 많은지이다.

Thurston은 3차원의 기하화 프로젝트 과정에서 virtually fibered conjecture라는 것을 제시하였다. 사실 Thurston이 참이라고 생각하면서 제시했다기보다는, 이것이 성립하면 너무 좋을 것 같다는 취지에서 제시한 것 같다. virtually fibered conjecture의 내용은, 이름에서 알듯이 모든 closed hyperbolic 3-manifold가 mapping torus 구조를 갖는 finite cover를 갖느냐는 것이다.

21세기에 들어서 Wise는 closed Haken hyperbolic 3-manifold에 대해서 virtually fibered conjecture가 참임을 증명하였고, 이후에 Agol이 closed hyperbolic 3-manifold가 virtually Haken임을 보임으로써 virtually fibered conjcture의 증명이 완성되었다.